|
L.R. Klein and S. Ozmucur* There is always uncertainty in connection with the estimation of a country's GDP and its rate of growth. There are problems of concept, missing data, incorrect reporting, sampling error where complete enumeration is not achievable, inconsistency of "mirror" statistics, and other pitfalls. The focus of the present investigation is the estimation of the annual growth rate of China's GDP and response to various critics who claim that recent reports are too high. First, let us consider some accounting issues, especially the facts that GDP measurement for any large and complex industrial economy is inherently difficult. There are at least three well-known accounting approaches to GDP measurement, and it is equally well-known (for several decades) that they rarely provide the same results. Method 1. GDP is the sum of final purchases. This is known as demand-side estimation and happens to be the officially favored method for the USA, but not for all nations. It finds textbook expression in the accounting definition. GDP = C(consumption)+I(investment) + G (gov't purchases) + X (exports) - M(imports) In input-output accounting, it is usually displayed in the form of column sums of a rectangular matrix at the rhs of the square inter-industry delivery matrix. Method 2. GDP is the sum of income payments to the original factors of production. It also is expressed in textbooks as GDP = W(wages)+IN(interest)+P(profits)+R(rent/royalty)+IT(indirect tax) - S(subsidy) In input-output accounting it is usually displayed as row sums of a rectangular matrix across the bottom of the square inter-industry matrix. Method 3. GDP is the sum of value-added across all sectors of production. Value-added is written as GP(gross production) - IP(intermediate production) = VA(value added) If all statistical reports were accurate and if all economic agents were cooperative respondents or reporters, these three methods should give identical estimates. The latest discrepancy between Method 1 and Method 2 for the USA, 2001, fourth quarter is estimated at $186 bn. (SAAR). While this is a small percentage of the (unknown) total GDP of the USA, it is a very, very significant amount. It is as large as many important national policy initiatives that are meant to stabilize the economy. It does not go away, and it is not a random series. It has a well-established serial pattern and is closely correlated with important economic variables.1 The nonrandom serial correlation found in data of the discrepancy between different measures of GDP for the USA has been found in other national data, but not always between Methods 1 and 2, but sometimes between 1 and 3. Some countries do not have full statistics for Method 2. It should be noted that there are similarities between Methods 2 and 3; they both aim for estimates of value-added, but Method 2 does this on an individual sector or industry basis, and Method 2 uses direct estimates of factor payments, while Method 3 derives factor payments (total or by sector) as a residual. It gets to value-added indirectly. This digression into different methods is to show, and to emphasize, that perfectly sensible approaches can provide estimates of GDP that differ by 1 or 2 percentage points, and since the discrepancy fluctuates, these differences in levels can affect "spells" of movement in growth rates. 2 China, at the time of early reform, 1978-1980, was just shifting from net material product to gross domestic product i.e. from Marxist to Western accounting. For their participation in Project LINK, Chinese econometricians made special efforts to estimate GDP as total values and not as refined constructs from input-output tables. Within LINK, we used the approximations to GDP that were given to us and also received guidance from Irving Kravis, who was gathering data for international comparisons in connection with the visit by the delegation of American economists under the auspices of the US National Academy of Sciences, American Council of Learned Societies, and the Social Science Research Council (the original sponsor of Project LINK). We had excellent rapport with statisticians from the Chinese Statistical Offices, who could fully appreciate the measurement needs for econometric analysis. Since Project LINK encountered similar problems with Soviet data and also had to convert from the concept of NMP to GDP, it may be fruitful to consider an extension of the original work of Sovietologists who were very inventive in studying the quantitative dimensions of the USSR. The scholars of the economy of the USSR used many proxies to get at Soviet aggregative measures. For output, they used volumetric statistics on coal, electricity, transportation, agricultural yields, and similar magnitudes. LINK regularly received excellent and helpful harvest estimates for grains, well in advance of forecast calculations for world economic activity. To study Chinese GDP from a fresh angle and test the consistency of China's GDP estimates with independent information, we assembled annual statistical series for the following magnitudes:
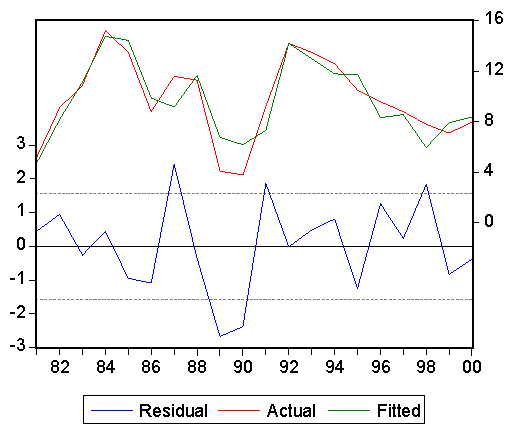
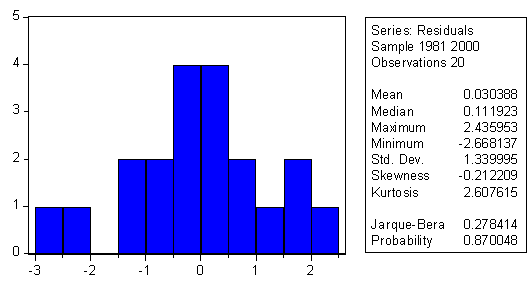
This gave us coverage of energy, transport, communications, labor, agriculture, trade, public sector, wage, inflation. Both the supply side, the demand side, and market mechanisms are featured in this array. In lieu of building a fresh macro model of the Chinese economy, we got very broad coverage in the form of a semi-reduced form. We estimated principal components (PCit) from annual data, 1980-2000, for these 15 indicators. The first three components account for 60.8% of the overall variance of the whole set. In addition, the 9th component accounts for another 2.6%, and has a large coefficient of oil in the corresponding eigenvector. A regression estimate of percentage change in GDP (the statistic in question) provides the following result
Each principal component is a linear combination of the 15 indicator variables listed above, each variable being expressed as an annual percentage change. The use of principal component analysis has figured prominently in this report. It is a technique that has been used a great deal in psychology and closely related social sciences to gain information on latent variables, such as intelligence measurement among individuals, based on identifiable characteristics and also for the purpose of data reduction. In econometrics, it has been used for reduction of large data collections into more manageable form, especially to deal with problems of multicollinearity and shortage of degrees of freedom. A very early use was introduced into econometric analysis by Richard Stone. 3 He used time series of separate group entries in the NIPA of the 1940s, and earlier, covering both the expenditure and income sides of the accounts. He extracted the first three principal components identifying one as National Income (NI) (the contemporary aggregative concept), one as change in NI, and one as chronological trend. He made this identification by examining the relative sizes of coefficients and by empirical correlation of components with the explicit aggregates. The main aggregate was implicit in the analysis, as the sum of income components. He made no attempt to deal with the statistical discrepancy between total outlay and income. Stone was able to make some inferences about headline aggregates, which are analogous to those that have been frequently examined in appraisals of the Chinese economy, namely, levels and rates of change of GDP, in line with the objectives of our present investigation. We, however, transformed all variables, both the headline statistics; as well as the individual indicator statistics; these transformations helped to deal with trend problems in residual error. Our objective has been to isolate "white-noise" residual variation from the "signal". Another motivation for using principal component analysis is our general point of view that a country's (any country's) economic growth is highly multivariate. No single measured economic activity can account for anything as complex as a modern economy, especially one as large as China's economy. We examined many time series, selected those that seemed to have a priori importance (leaving us with 15) and only 20 annual data points. In order to conserve degrees of freedom we narrowed the list of rhs variables in the regression to no more than four (principal components). This has been an important motivation in adopting the principal component methodology. What is more, these components account for a high degree of variation of the total set. Also, by construction, the components are mutually uncorrelated; therefore we can handle the multicollinearity problem from a statistical point of view. Each component depends, in some way or another, on the whole set of indicators, yet their intercorrelation, which is naturally high, does not confound the interpretation of the regression estimates, and we have plausible associations between GDP growth and individual indicator growth, as estimates in Table 1. In a recent paper, the Indian statistician and econometrician, A.L. Nagar, with Sudip Ranjan Basu, has suggested the use of principal components to investigate human development, much as UNDP estimates its "Index of Human development". 4 Nagar measures various indicators, beyond the UNDP listing, across countries, and extracts principal components. He then forms weighted averages of the components, with weights being the eigenvalues of the principal component analysis. He then declares that this weighted value represents human development, different for each country because the country indicators are different. He does not have a measured quantity, such as GDP growth rate estimates, to correlate with the principal components. That is the meaning of the term latent variable analysis. To a large extent, we have followed the pathways laid out by Stone and Nagar, but we have adapted their methodology to the specific case of estimating China's economic growth rate. How can one interpret this numerical statistical finding? The principal components reflect, in a generalized sense, the movement of 15 broadly based measures of the Chinese economy collected quite independently from diverse sources. The movements of these summary indicators, the principal components, are consistent with the movements of real GDPt as officially estimated. It cannot be claimed that we have proved that GDPt as officially measured is correct. No one knows the correct estimate; that is the whole point of showing how different such estimates can be, depending on how they are calculated, and this is true the world over. Not only are the movements of GDP and the combination of PC values highly correlated, but the relevant regression estimate has serially uncorrelated errors (both Durbin-Watson and Breusch-Godfrey tests). Also there is no apparent heteroskedasticity of residuals and the correlogram of residuals from the regression is confined to narrow bands. The coefficients of the regressions and in the eigenvectors are both positive and negative, but as we have calculated in Table 1, they are all positively related, at the margin, to GDP. When Irving Kravis first estimated the level of Chinese GDP per capita, at the beginning of the reform period, there was significant criticism, much of it coming from Chinese scholars. He collected just under 100 prices, over a short time span. The visiting team did, however, go to as many as six sites, both rural and urban. He also had some independent information about medical care and education costs from other visiting experts in those fields. After a few years of reform, economists, statisticians and political people became aware of the significant growth achievements of China and great attention was paid to Kravis' figure, which placed China approximately equal to the Philippines (and double the Indian position) scaled as a percentage of the US per capita income level. Also, the returns of the 1980 Census, which was being taken at the beginning of reform, indicated that a modest per capita figure, when multiplied by a huge total population figure, placed China very high in the world ranking of total GDP. At this time, in the mid-to-late-1980s it was also found that China's growth rate (percentage change in either total or per capita GDP) was reduced if evaluated at world prices, i.e. using PPP conversion factors rather than market exchange rates. At the same time, when some international institutions were forming weighted averages of country growth rates, to get average world rate, the inclusion of developing countries, including China as one developing country, produced world rates that were larger than if weighted by shares in GDP that were evaluated at market rates. Chinese growth at constant world prices is biased downwards in comparison with evaluation at market or official exchange rates. This bias was also found by Alan Heston, Daniel Nuxoll, and Robert Summers in a large cross-country sample that compared, for each country, two ways of computing growth -- using base period world prices, or using base period "own" prices. They found that poorer developing countries grew more slowly, using world prices. China was not in their sample, but would, by inference, show lower growth when evaluated at base period world prices. 5 As long ago as World War II, economists and statisticians in Great Britain argued that the cost-of-living price index had a downward bias because it did not allow for the substitution effect of shifting towards relatively more unrationed goods in place of rationed goods in the household budget. The former (unrationed goods) were inferior to the latter (rationed) goods. There was a loss of real income by using a price index deflator that did not take rationing into account. After World War II we were quickly exposed to the opposite bias in the consumer price index because new goods that were built on the advanced technologies of the postwar era were of superior quality. One of the first major acknowledgments of this concept was in the estimation of the price of motor cars. A typical quality factor was the availability and rapid addition of the "automatic gear shift". The method of hedonic index number construction made specific allowance for some types of quality change; this tended to reduce price index values below where they would have been, and provided adjusted real output calculations for faster growth. On an increasing scale, quality improvements were introduced, and the Boskin Commission in the United States added up to approximately ½ percentage point of growth to US GDP, by adjusting the consumer price index for improvements in computer and other quality changes. The higher speeds, enlarged capacity, and added friendliness of the computer made its adjusted price decline, in the midst of rising prices elsewhere. In the China case there has been enormous quality change since 1978-80, when economic reforms were introduced. The diet is vastly improved; clothing is much better and varied; the motorcar fleet is remarkably improved; aircraft seat-miles are modernized; education is far better at all levels; housing is improved; tourist facilities are closer and closer to world standards; communication is better; and one could go on, endlessly, describing the quality changes. In short the Chinese "market basket" is of such far greater quality in comparison with the start of reform that there is surely a need for a major adjustment in price indexes -- even larger than the quality improvements that have already been introduced in the US and other Western economies. For anyone who has regularly visited China, year-by-year since the start of reform, the quality aspect of Chinese economic life is quite apparent and "crying out" for a major statistical investigation to measure its growth impact. The construction of relevant hedonic indexes as well as complete expenditure systems are needed in order to carry the investigation forward in a careful empirical mode.
APPENDIX A: MAIN ECONOMIC INDICATORS FOR CHINA (CONTINUED)
APPENDIX B PRINCIPAL COMPONENTS
PRINCIPAL COMPONENTS (CONTINUED)
PRINCIPAL COMPONENTS (CONTINUED
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||